Diffusion

At first sight, diffusion is not connected to HSP. There is no mention of HSP Distance in any equation of Fickian diffusion!

However, it quickly becomes clear that the two are intimately connected. First, diffusion rates depend on concentration gradients. And if, say, a solvent is hardly soluble in a polymer there will only be a small concentration gradient. Second, the diffusion coefficient depends on the concentration. If a solvent swells a polymer then the diffusion coefficient in that swollen polymer will be much higher (orders of magnitude) than the coefficient in the pure polymer. In other words, the smaller the HSP Distance between a solvent and a polymer the larger the concentration gradient, the larger the concentration and the larger the diffusion coefficient.

The science of each of these issues is discussed step-by-step in the specific Diffusion apps, along with the complication of surface resistance which certainly slows absorption to high concentrations or evaporation from solutions in film formation, for example. In some relatively rare circumstances surface effects can slow down absorption even for very low final concentrations. But there is an historical anomaly to clear up. Many people think that "anomalous diffusion" requires novel mechanisms. As this page will show, that is simply not the case. The text below is Charles' personal views but the HSPiP team fully support what he says as the HSPiP Diffusion modeller and the apps on this site can be used to verify what follows.

Anomalies of diffusion? No!

The diffusion equation says it all. There has been a great deal of discussion in the literature about “anomalies” of diffusion in polymers. I have not found any anomalies. This is true for absorption as well as for desorption (film drying). Appropriate solutions to the diffusion equation, Fick’s second law, describe all of these. Evidence for this is found in the second edition of my CRC handbook Hansen Solubility Parameters: A User's Guide in Chapter 16 and earlier publications. The diffusion equation is a second order partial differential equation that requires two boundary conditions and an initial condition for solutions. The diffusion equation is derived in a very general way. There is no problem involved with using concentration dependent diffusion coefficients or a surface condition. The fact that diffusion coefficients can vary by a factor of a million or more within a limited concentration range is therefore no problem. Boundary conditions can be chosen to account for important physical phenomena at the film surface. A significant surface resistance can be caused by factors exterior to the film surface itself such as rate of heat transfer, air velocity, diffusion in a stagnant air film, and the like. The mass transfer coefficients are relatively high, but can still be significant if diffusion within the film is rapid. A significant entry resistance may be found within the film surface itself and is caused by the morphology of the polymer in the surface. The mass transfer coefficient in such a case is very low. This surface morphology can be a result of rapid cooling after an injection molding processing or just be natural to given polymer types where larger and bulkier molecules have difficulty finding an adsorption site from which to subsequently absorb into the bulk of the film. Both surface resistance and entry resistance are described by the same kind of boundary condition for solutions to the diffusion equation. Some definitions follow:

Fickian Diffusion usually means that there is a straight line describing the uptake of a liquid or gas into a polymer film when the amount taken up at a given time is plotted against the square root of time. The straight line passes through the origin. This is common and expected when the diffusion coefficient is constant or nearly so, and there is no surface or entry resistance.

The S-Curve Uptake “anomaly” involves delayed absorption. A plot of amount uptake versus the square root of time does not produce a linear relation that passes through the origin. The reason for this delay is a surface or entry resistance that has become significant relative to the diffusion resistance. The surface or entry resistance is expressed by the inverse of the mass transport coefficient (1/h), and the diffusion resistance is given by the film thickness divided by the diffusion coefficient (L/D). Their ratio has been called B = hL/D and can be used in generalized solutions to the diffusion equation. S-curves are readily generated by solutions to the diffusion equation with a boundary condition that accounts for significant surface or entry resistance.

Case II diffusion is the term generally applied to a linear uptake of solvent using a plot of amount absorbed versus linear time (not square root of time). This is obviously a deviation from the terminology discussed above for Fickian diffusion. This behavior is described by appropriate solutions to the diffusion equation, however, and is found when the diffusion coefficient is very dependent on solvent concentration. The diffusion coefficient in rigid polymers increases by a factor of about 10 for each additional 3 percent by volume solvent that is locally present. In elastomers the diffusion coefficient increases by a factor of approximately 10 for each additional 15 percent by volume of solvent. There is a limit to this rule of thumb when the solvent concentration approaches 100% and the diffusion coefficient approaches the self-diffusion value.

As the name indicates, Super Case II is a modification of the Case II type behavior that has just been discussed.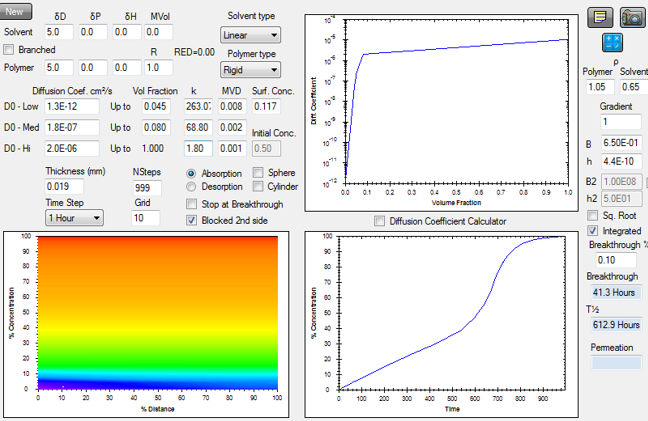
Figure: Matching the Super Case II experiments of Hopfenberg and coworkers using concentration dependent diffusion coefficients and a significant, experimentally confirmed surface resistance¹.
In this case the uptake is initially linear on a plot using linear time, but at some time well into the absorption process, the rate of uptake suddenly increases. An explanation for this astounding behavior has challenged many and there are many explanations. Since straightforward solutions to the diffusion equation can readily describe this behavior as well as all of the above, I see no reason to be surprised. An example from the HSPiP Diffusion modeller is given in the figure. This figure confirms that one can reproduce Case II type behavior when a significant entry resistance is combined with a concentration dependent diffusion coefficient. The diffusion coefficient varies with concentration as shown in the upper right figure. These values were required to match the curvature in the uptake curve. Solvent retention in the sample has led to a more rapid increase of the diffusion coefficients with concentration than otherwise expected. The surface condition in this case involves an entry resistance and not an effect external to the film surface. This is described by the given B and h values in the figure. The h required to match the experimental uptake curve agrees very well with that derived from the initial rate of uptake that was reported for the experiment. The concentration gradients that develop as a function of time can be seen at the lower left. They are horizontal and not vertical as many would have suspected. The absorption curve is plotted as a function of linear time showing the very dramatic increase in the rate of uptake well into the absorption process. The reason a constant h describes this and other absorption experiments is thought to be that the polymer chain segments at the surface continue to orient in the same way toward the external phase regardless of the concentration profile in the bulk. Since this surface orientation is controlled by HSP affinities, the intimate relation between diffusion in polymers and HSP discussed above is reinforced by this effect as well.

Conclusion

The conclusion to be drawn from the above, based on careful measurements published in reviewed journals, is that there are no “anomalies” in diffusion in polymers. One need only solve the diffusion equation for absorption or desorption with the verifiable coefficients to reproduce the behavior that is measured and described by the various terminologies. The diffusion equation can equally well describe Fickian absorption or desorption, S-curves in absorption, Case II, Super Case II, and even the drying of a lacquer film where the concentration of the evaporating (desorbing) species falls from very high, with very high diffusion coefficients, to zero, where the diffusion coefficient has fallen by many orders of magnitude.

There are no anomalies in diffusion in polymers. This has been confirmed by the software provided in HSPiP and also in the Diffusion apps. Specific data in literature reports reporting such generally accepted anomalies are treated in detail in downloads found elsewhere on this website. These were analyzed with the HSPiP software.